Parametrização com métodos gráficos
Uma forma de se determinar a estrutura do modelo é observando a resposta do processo a um teste em malha aberta. Neste teste, o processo é submetido a uma entrada “perturbadora”, que o força a revelar sua dinâmica. Este sinal de entrada pode ter o formato de um impulso unitário, um degrau, um pulso, entre outros. O mais comum é o uso do teste ao degrau.
Clique sobre a figura abaixo para assistir ao vídeo:
Teste de resposta ao degrau em malha aberta
Na modelagem “caixa-preta”, testes devem ser realizados sobre o processo para identificar a relação dinâmica entre entrada e saída. Estes testes devem produzir sinais de entrada que “perturbem” o processo. Sua resposta irá revelar seu comportamento dinâmico.
No teste em malha aberta (MA), o controlador é colocado em modo manual (chave seletora na posição “M”) e novos valores para a MV são definidos manualmente.
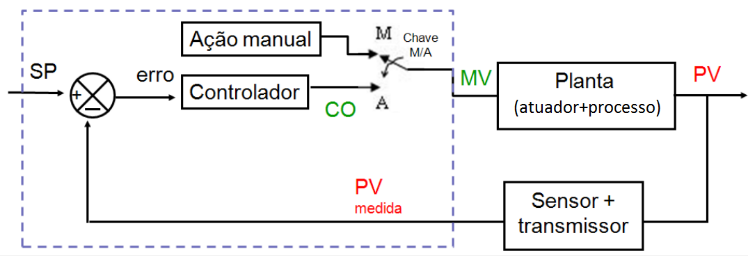
A cada novo valor atribuído a MV significa um degrau sendo enviado ao processo cuja resposta é refletida na PV. Durante os testes os sinais de entrada (MV) e de saída (PV) devem ser registrados para posteriormente serem utilizados na parametrização do modelo matemático. 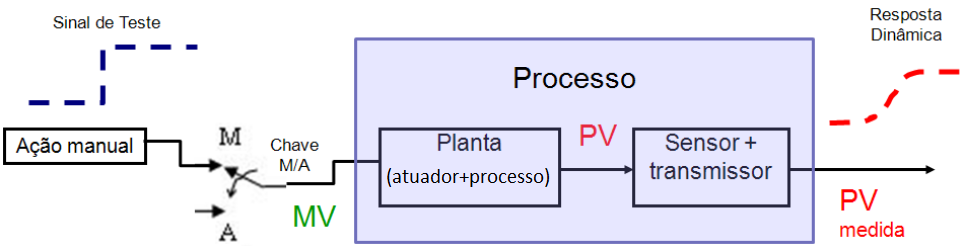
Vale notar que a relação entre MV e PV engloba os efeitos dinâmicos de todos os elementos de campo existentes entre a saída do controlador e a medição da PV, tais como: atuadores, redes de comunicação, elemento sensor e transmissor e o processo a ser controlado (forno, tanque, vaso de pressão, etc).
Seleção do tipo de modelo a partir do perfil da resposta ao degrau
Alguns perfis de resposta ao teste de resposta ao degrau são apresentados abaixo junto com a função de transferência correspondente.
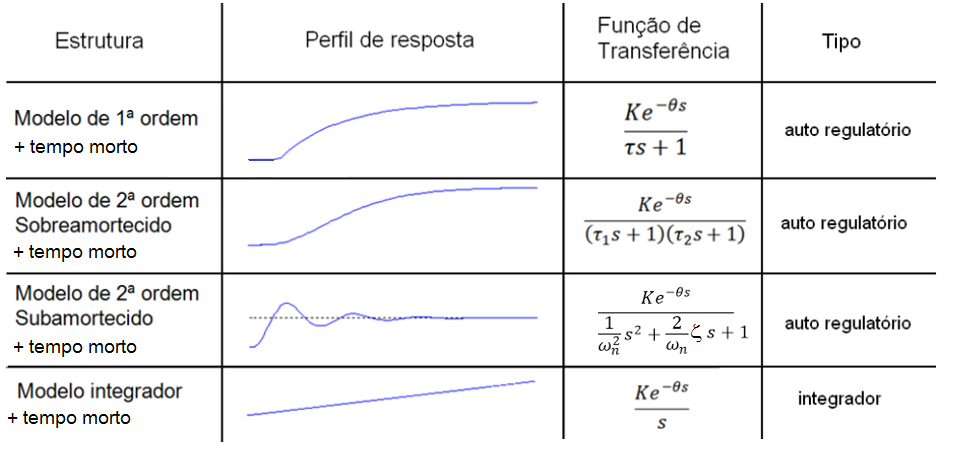
Processos que estabilizam num novo patamar depois de submetidos a um teste em degrau são chamados de Processos Auto Regulatórios. É o caso dos três primeiros. Apresentando uma resposta que cresce ou decresce linearmente, temos o Processo Integrador e, se a resposta cresce exponencialmente, temos um Processo Instável.
Parametrização de modelo de 1ª Ordem
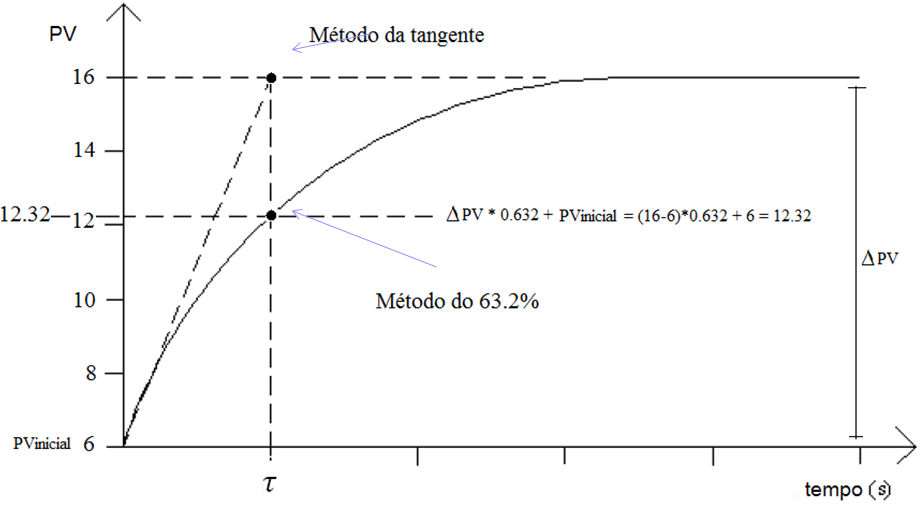
O modelo de 1ª ordem com tempo morto, também conhecido com (FOPDT – first order plus dead time), é um modelo que possui um único polo real, é parametrizado por um ganho estático (K), um tempo morto (q) e uma constante de tempo (τ). Sua função de transferência tem a estrutura mostrada abaixo:
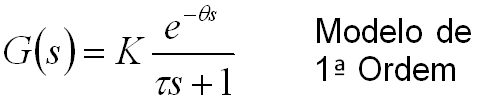
- ganho (K): é a razão entre a variação total da PV e a variação na MV. Para um resultado adimensional, PV e MV devem usar escalas normalizadas.
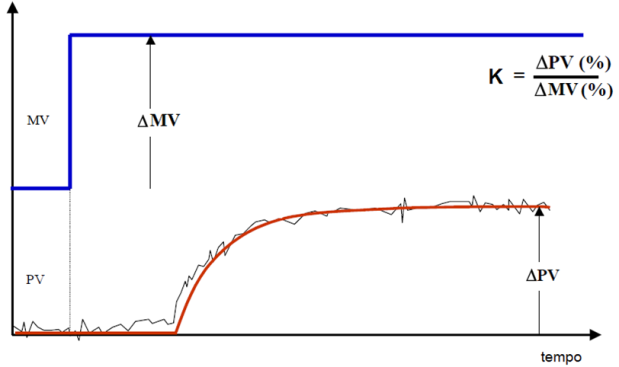
- tempo morto (θ): É o intervalo de tempo entre o instante do início do teste (degrau na MV) e o instante em que a PV começa a manifestar sua resposta ao teste.
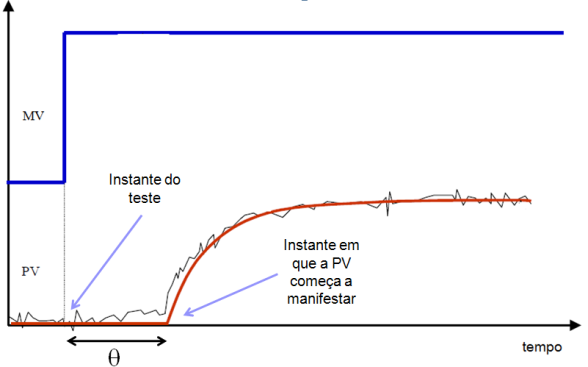
- constante de tempo (τ): Pode ser obtida calculando-se o intervalo de tempo entre o instante que a PV começa a reagir até o instante em que ela atinge 63,2% de sua variação total. (“método do 63%”). Uma forma alternativa é traçando-se uma tangente ao início da curva e marcando o instante em que esta tangente intercepta o valor final da PV (“método da tangente”).
Parametrização de modelo de 2ª Ordem sobreamortecido
Harriot observou diversas curvas da resposta normalizada (y/K) em sistemas de segunda ordem para diferentes frações de τ2/τ1, e encontrou que todas as curvas se interceptam aproximadamente a 73% do valor final. Neste ponto, também observou que a razão t/(τ1+ τ2) é igual a 1.3 como se mostra na figura:
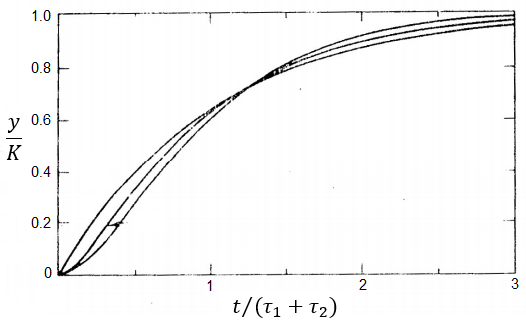
Harriot, por meio de diversos dados experimentais, também confrontou a magnitude de y com os instante de tempo dado pelas razões τ1 /(τ1 +τ2) e 0.5/(τ1 +τ2), obtendo funções específicas e elaborou o seguinte procedimento:
- Na resposta com magnitude normalizada (y/K), medir o instante em que y atinge 73% do valor final (t73).
- Calcular o valor da soma das constantes de tempo: (τ1 +τ2) = t73/1.3
- Novamente no gráfico de resposta, medir o valor de y no instante t = 0.5(τ1 +τ2)
- Com o valor de y obtido no item anterior, obter o valor da relação τ1 /(τ1 +τ2) por meio do gráfico abaixo:
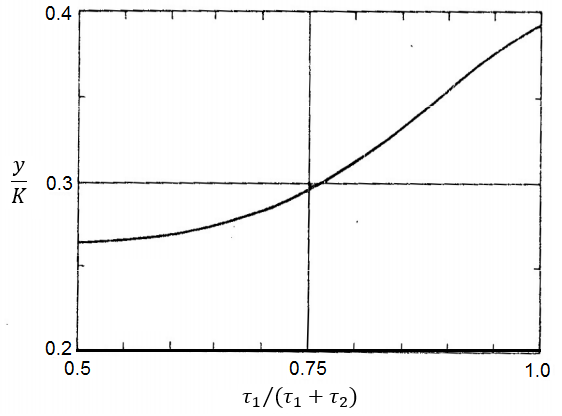
- Como a soma (τ1 +τ2) já é conhecida, então é possível obter τ1 e τ2
Exemplo: Considere a resposta de um sistema de segunda ordem mostrado abaixo (com a magnitude já normalizada):
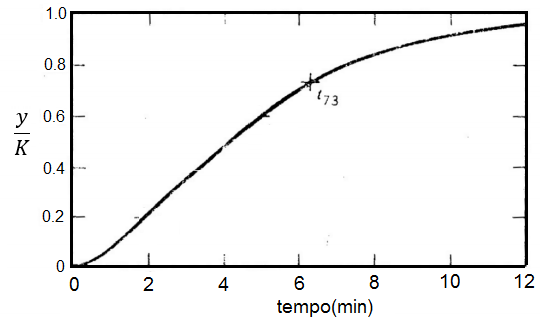
- Observa-se no gráfico de resposta que: t73 = 6,4 min
- E então: (τ1 +τ2) = t73/1.3 => (τ1 +τ2) =4,92 min
- E o valor de y no instante t = 0.5(τ1 +τ2) = 2,46 min é aproximadamente y=0,295
- Observando o gráfico experimental, temos que para y=0,295 temos τ1 /(τ1 +τ2)=0,74
- E como (τ1 +τ2) =4,92 se obtém τ1 = 3,64 min e τ2 = 1,28 min
Parametrização de modelo de 2ª Ordem subamortecido
No caso da resposta se assemelhar a um modelo de 2ª ordem subamortecido, quatro parâmetros devem ser identificados: o ganho K, o tempo morto (θ), o fator de amortecimento ζ e a frequência natural de oscilação ωn.
A função de transferência tem o formato:
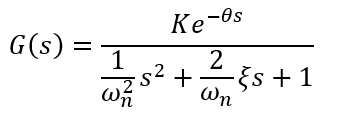
Os parâmetros K e θ são obtidos de maneira idêntica ao que foi apresentado para modelos de 1ª ordem. Já a frequência natural corresponde ao inverso do período aparente de oscilação (T), multiplicado por 2*pi. Já o fator de amortecimento pode ser aproximado, conforme proposto por Phillips e Parr (1991), pela relação mostrada abaixo. Onde NC corresponde ao número de ciclos visíveis.

O exemplo a seguir mostra a resposta de um sistema a um degrau unitário. O sistema é de 2ª ordem subamortecido, com ganho K unitário e com tempo morto desprezível. É possível observar 4 ciclos e meio de oscilação, sendo que os quatro primeiros ocorrem nos primeiros 25 segundos, assim temos:
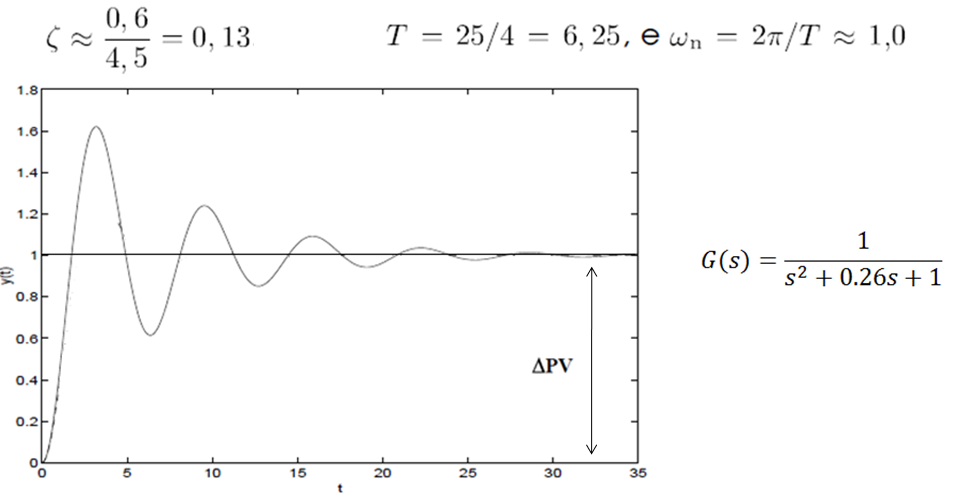
Parametrização de modelo integrador
Em processos integradores, a saída (PV) é proporcional a integral da entrada (MV). O ritmo de integração é dado pela constante , chamada de ganho integrador. Considera-se também a existência de possíveis atrasos de transporte. Assim temos a seguinte função de transferência:
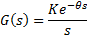
O parâmetro θ(tempo morto) é obtido da mesma forma que nos métodos anteriores. Já o ganho Ki corresponde a razão entre a mudança de inclinação na PV e a amplitude do degrau de entrada que causou esta mudança de inclinação.
A seguir um exemplo de cálculo dos parâmetros e q, sendo a e b as inclinações de y antes e após o degrau, respectivamente.
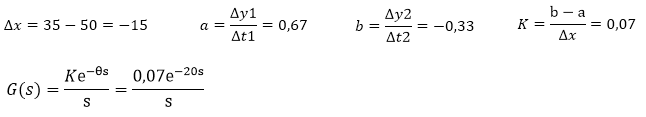
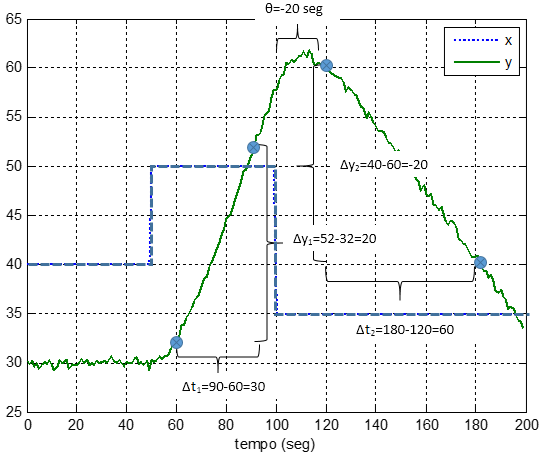
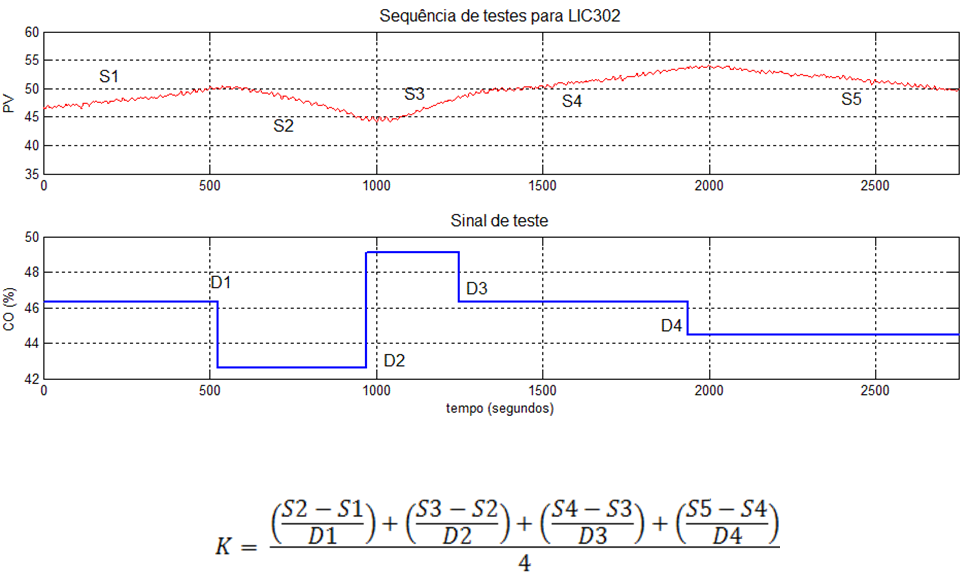
Um resultado mais preciso será obtido se a constante Ki for obtida pela média de diversos testes em sequência. No exemplo a seguir são quatro mudanças em degrau na variável manipulada, e quatro mudanças correspondentes na inclinação na PV. O ganho integrador é obtido pela média dos ganhos.