Método computacional

Retorna para tópico anterior

Avança para próximo tópico

Considere a obtenção de um modelo matemático de um processo G(s), por meio de um teste ao degrau em malha aberta. O primeiro passo é determinar uma estrutura para o modelo, dos quais os mais usados são: primeira ordem com tempo morto e segunda ordem com tempo mordo, conforme mostrado abaixo.

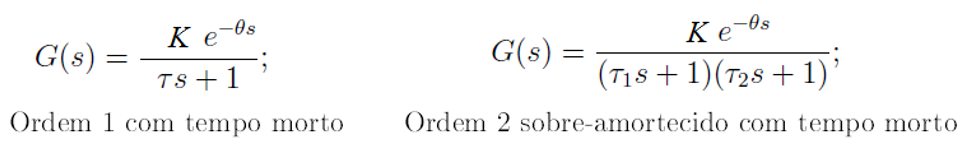
O próximo passo é fazer a parametrização do modelo, ou seja, obter os valores de K, θ e τ para o modelo de primeira ordem e os valores K, θ, τ₁ e τ₂ no modelo de segunda ordem. Um critério comum é escolher os parâmetros que resultem na curva que melhor se ajusta aos dados reais. Por exemplo, a figura abaixo mostra a resposta de um teste ao degrau realizado num processo e as curvas representando dois modelos propostos.

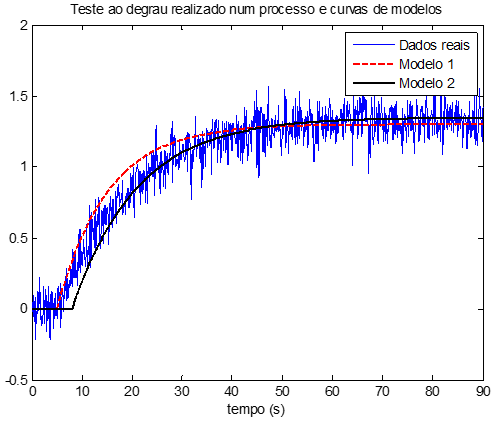
Qual das curvas se ajusta melhor, o do modelo 1 ou a o modelo 2? Uma forma de responder essa questão é somando, para cada instante de tempo, o erro quadrático entre os dados reais e os dados fornecidos pelo modelo, utilizando a expressão:

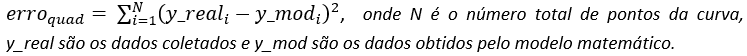
O melhor modelo é aquele que possui o menor erro quadrático. Este artigo apresenta um algoritmo em Matlab® capaz de fornecer os parâmetros de um modelo que resultam no menor erro quadrático possível.

Algoritmo MATLAB para modelo de primeira ordem

O algoritmo mostrado abaixo permite obter os parâmetros ótimos para um modelo de primeira ordem. Os dados são inicialmente carregados em dois vetores: “pv” contem os dados da variável controlada e “t” o vetor tempo. A variável delta_MV deve ser inicializado com a amplitude do degrau na MV. Outra consideração importante é eliminar no arquivo de dados os valores antes do início do testes (manter apenas os dados a partir do início do degrau). Antes de chamar a função de otimização “pminsearch”, deve-se inicializar o vetor de parâmetros p0 com valores razoáveis para o ganho, constante de tempo e tempo morto. Isso garante a convergência da função de busca.

%normalização da PV. Dividindo-se a PV por delta_MV, temos a resposta ao degrau unitário
pv = pv-pv(1);
pv = pv/delta_mv;
%vetor com valores iniciais para o modelo
%p0 = [ganho tal tempo_morto]
p0 = [1 5 2]; %vetor com valores de chute inicial para o modelo
p = fminsearch(‘erro_med1’,p0); %chamada da função de otimização

Repare que o primeiro parâmetro da função de otimização “pminsearch” é uma função que retorna o valor do erro quadrático a partir dos parâmetros do modelo (erro_med1). Seu código é mostrado logo a seguir.

function V=erro_med1(p)
% obtem resposta do modelo “y_mod”
Kp = p(1);
tal = p(2);
atraso = p(3);
G = tf(Kp,[tal 1]);
G.inputdelay = max(atraso,0);
pv_mod=lsim(G,mv,t);
%calcula erro médio quadrático
erro = pv-pv_mod;
V = mean(erro.^2);

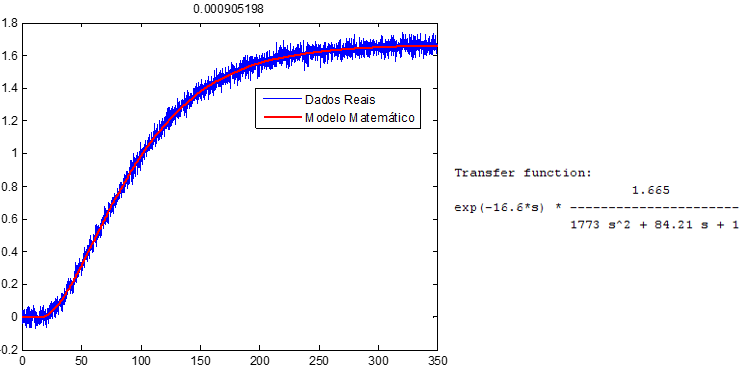
A figura a seguir mostra um exemplo de utilização destas rotinas. O modelo matemático obtido contém os melhores parâmetros possíveis para seu ajuste com os dados reais.

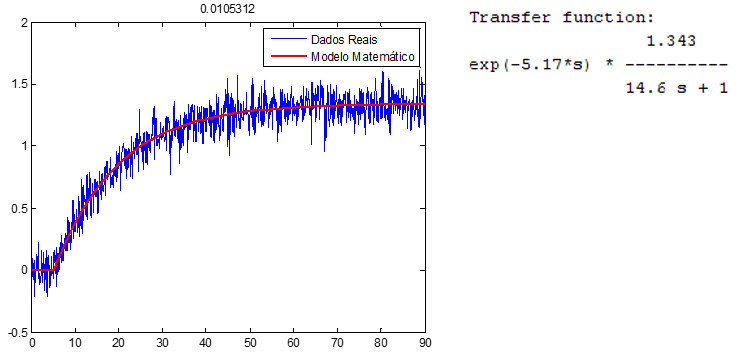
Algoritmo MATLAB para modelo de segunda ordem

Este algoritmo é similar ao anterior, porém permite obter os parâmetros ótimos para um modelo de segunda ordem com tempo morto. Portanto seu vetor de parâmetros p0 contém 4 elementos [ganho tal1 tal2 tempo_morto]. Da mesma forma que o algoritmo anterior, os dados devem ser salvos em vetores “pv” e “t” e p0 deve ser iniciado com valores próximo aos reais.

%normalização da PV. Dividindo-se a PV por delta_MV, temos a resposta ao degrau unitário
pv = pv-pv(1);
pv = pv/delta_mv;
%vetor com valores de chute inicial para o modelo
%p0 = [ganho tal1 tal2, tempo_morto]
p0 = [1 35 35 20];
p = fminsearch(‘erro_med2’,p0);%chamada da função de otimização

A função “erro_med2” utilizada como parâmetro em fminsearch é mostrada a seguir:

function V=erro_med2(p)
% obtem resposta do modelo “y_mod”
Kp = p(1);
tal1 = p(2);
tal2 = p(3);
atraso = p(4);
G = tf(Kp,[tal1*tal2 tal1+tal2 1]);
G.inputdelay = max(atraso,0);
pv_mod=lsim(G,mv,t);
%calcula erro médio quadrático
erro = pv-pv_mod;
V = mean(erro.^2);

A figura a seguir mostra um exemplo de utilização destas rotinas. O modelo matemático obtido, que é de segunda ordem, contém os melhores parâmetros possíveis para seu ajuste com os dados reais.