Projeto domínio da frequência
Tempo de acomodação, tempo de restabelecimento, tempo de reação são exemplos de métricas temporais aplicáveis tanto em projeto como em avaliação de desempenho de controladores. Servem para qualificar o comportamento da malha diante de uma mudança de carga ou variação em degrau no setpoint.
No entanto, distúrbios e mudanças de setpoint nem sempre ocorrem em formato degrau. Uma malha de controle pode ter como requisito, por exemplo, a capacidade de rastrear um setpoint senoidal com frequência de 0,03 Hz ou ter a capacidade de compensar 90% de um distúrbio de natureza aleatória, mas com espectro de potência conhecido.
Estas duas situações são ilustradas abaixo.
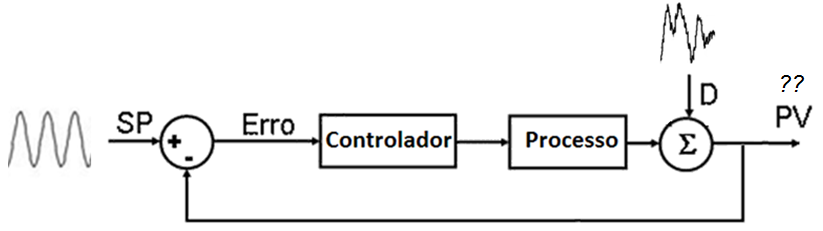
Nestes casos o projeto do controlador deve seguir critérios no domínio da freqüência, tais como banda de passagem, banda de rejeição, freqüência de corte, período de corte.
Sinais senoidais e sistemas dinâmicos lineares
Quando um sinal senoidal é aplicado na entrada de um sistema dinâmico linear, obtêm-se na saída um sinal também senoidal e com a mesma freqüência. As únicas propriedades que podem ser alteradas são amplitude e fase.

As alterações na amplitude e fase são quantificada pelas funções AR(ω) e Φ(ω), chamadas de funções de resposta em frequência, específicas para cada sistema.
No caso de um sinal de entrada não-senoidal, as funções de resposta em frequência ainda são aplicáveis desde que esse sinal seja previamente transformado em um espectro de frequência. Um exemplo é o uso da série de Fourier para transformar um sinal periódico qualquer em uma combinação de ciclos senoidais.
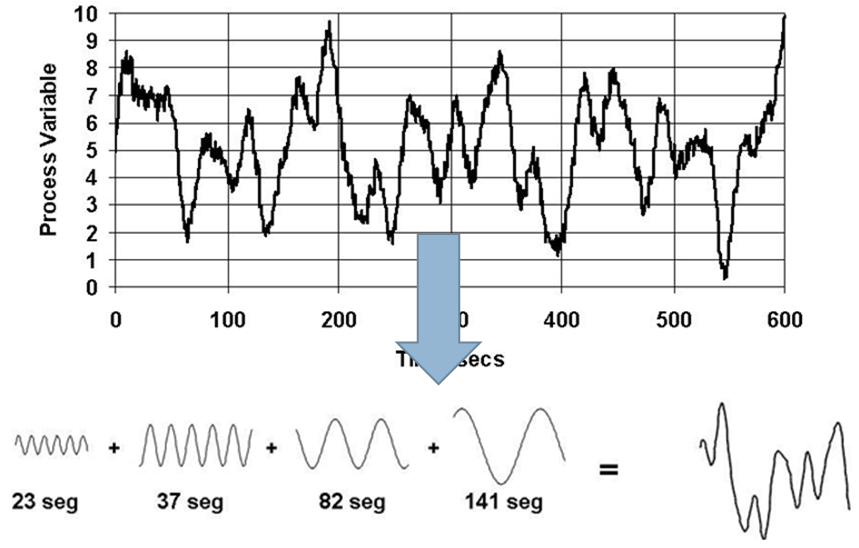
Desta forma, é possível determinar como uma entrada irá afetar a saída de um sistema G(s) se forem conhecidas suas funções de resposta em frequência AR(ω) e Φ(ω).
A figura abaixo mostra um sinal não-senoidal sendo aplicado a um sistema dinâmico. Primeiramente este sinal é transformado em espectro de frequência e os quatro ciclos mais importantes (com maior energia espectral) são analisados separadamente. Para cada um é calculado a amplitude e fase do seu ciclo correspondente da nsaída baseado nas funções AR(ω) e Φ(ω) do sistema. Por fim, é feita uma transformação inversa do espectro de frequência do sinal de saída para sua versão no tempo.
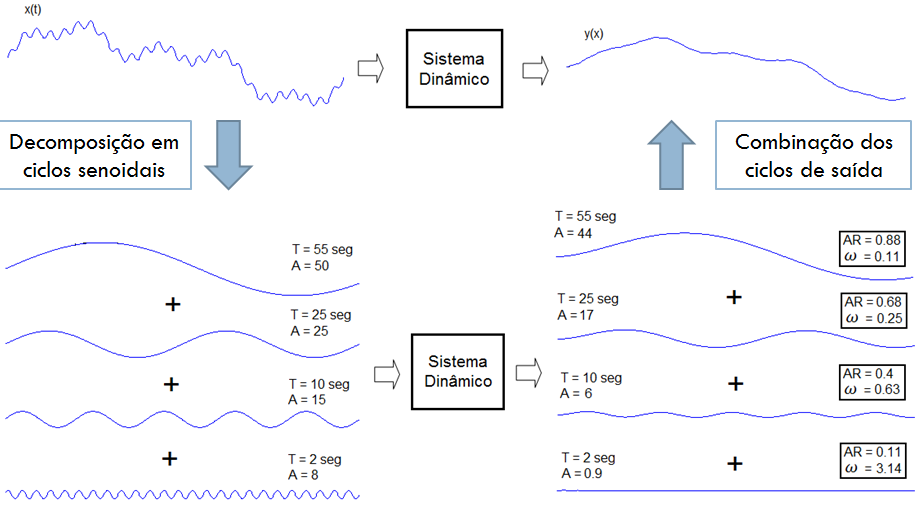
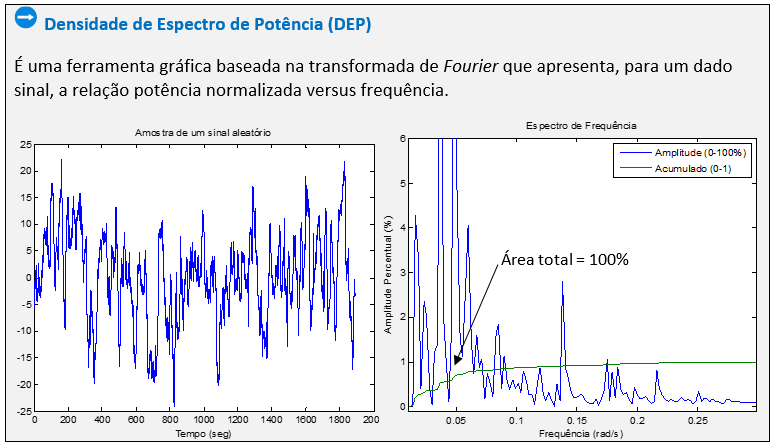
Resposta em freqüência de sistemas dinâmicos lineares
Se a função de transferência descreve a relação entrada-saída de um sistema no domínio de Laplace, as funções de resposta em frequência AR(ω) e Φ(ω) fazem o mesmo para sinais senoidais (ou componentes do espectro de frequência de um sinal não-senoidal). E estas funções podem extraídas da própria função de transferência.
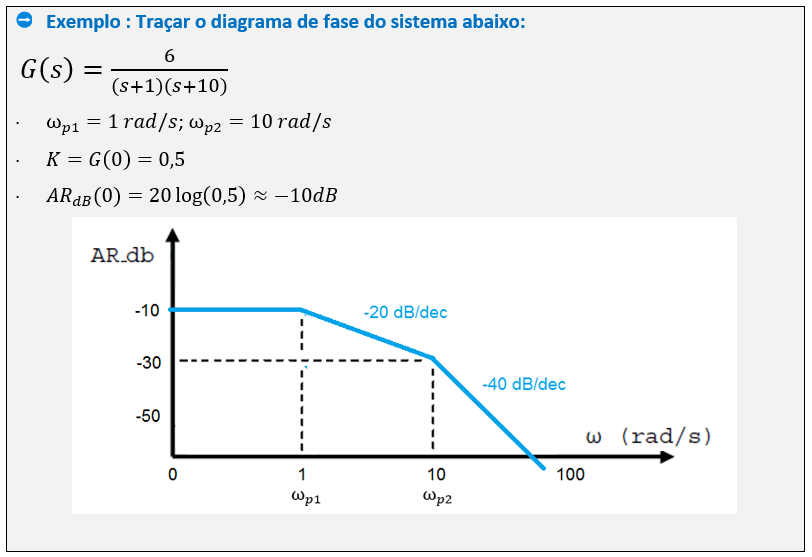
Considere o sistema:
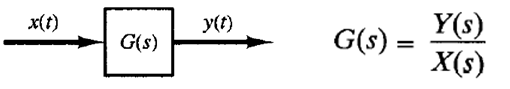
A funções de resposta em freqüência podem ser obtidas diretamente de G(s), substituindo o operador de Laplace s, pelo operador jω. Em seguida, deriva-se AR(ω) do módulo de G( jω) e Φ(ω) da fase.
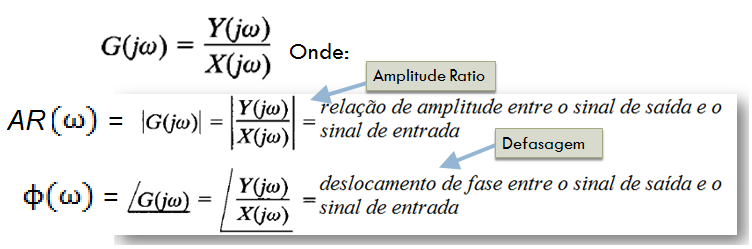
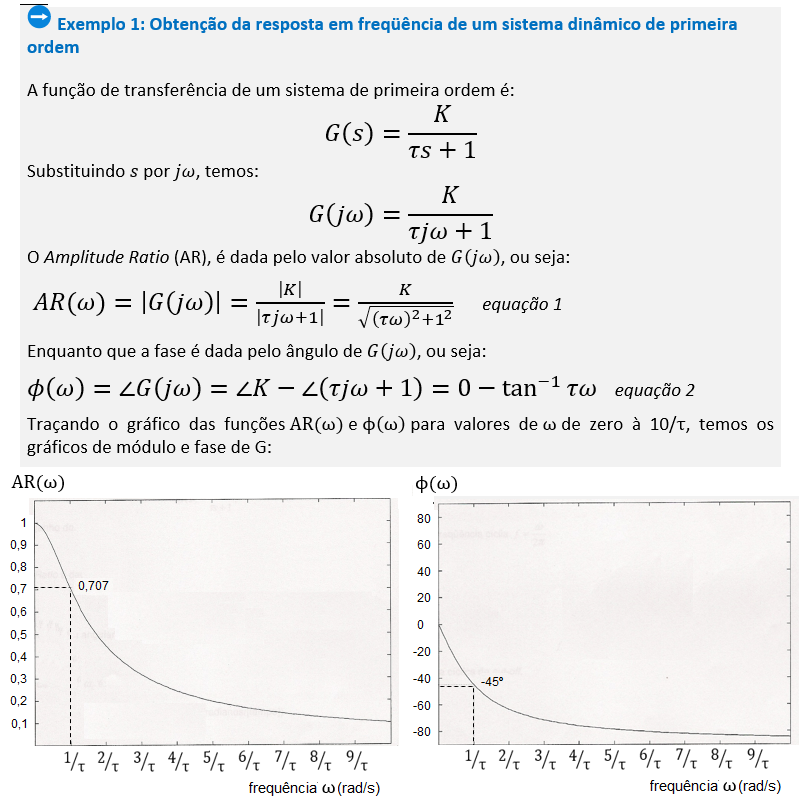
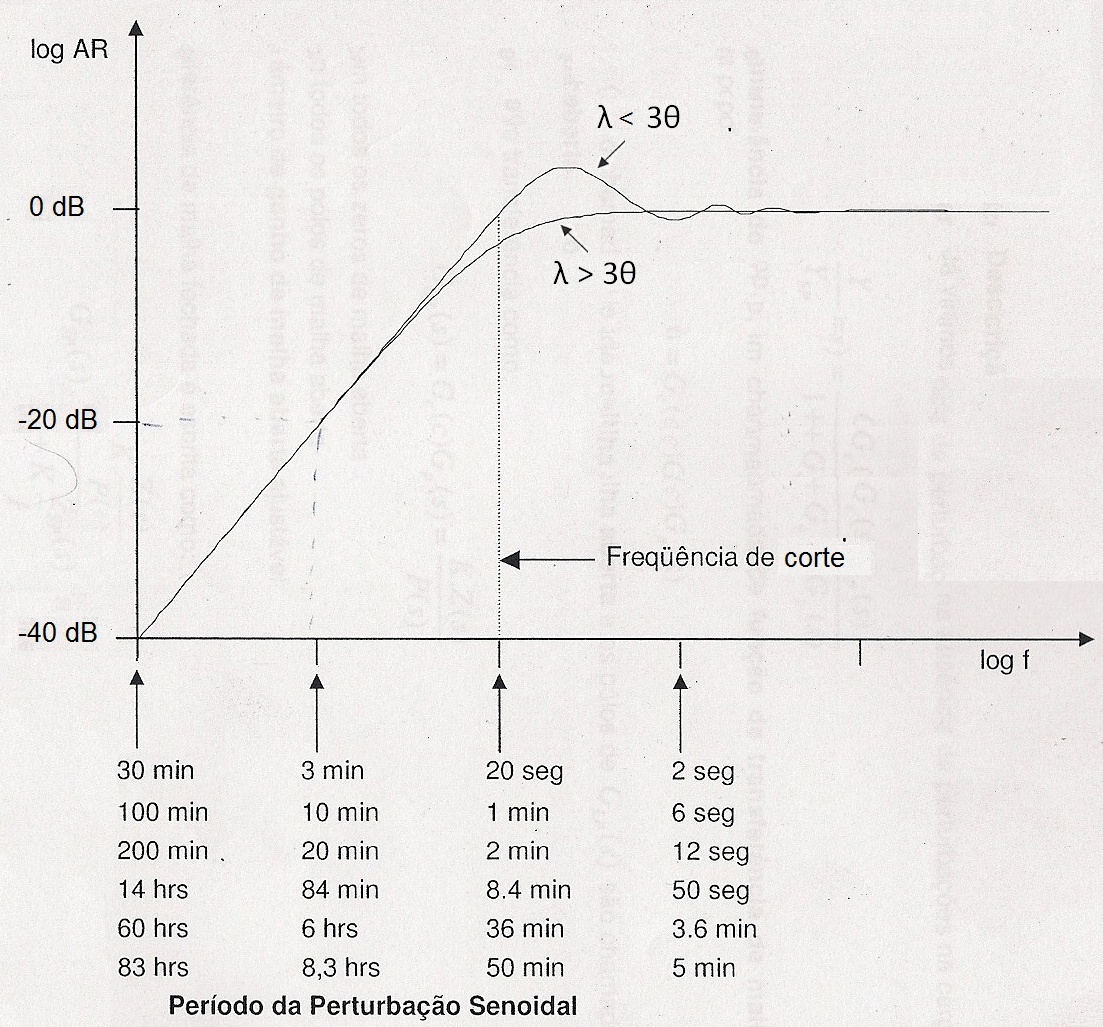
Um ponto de referência usualmente utilizado nas curvas de resposta em freqüência é a freqüência de corte ( ) ou freqüência de cut-off. Ela é dada em radianos por segundo e, em sistemas de primeira ordem, corresponde à freqüência do pólo do sistema, ou seja, é o inverso da constante de tempo. Podemos referenciá-la também como freqüência de corte em hertz e período de corte em segundos, após as seguintes conversões:


Diagrama de Bode
Traçar manualmente os gráficos das funções de resposta em frequência AR(ω) e Φ(ω) é bastante trabalhoso, especialmente em sistemas de ordem elevada. Um alternativa é usar usar o Diagrama de Bode, uma versão simplificada que aproxima as funções de resposta em frequência com segmentos de retas com inclinações padronizadas.
- Procedimento para o diagrama de Módulo.
No gráfico de módulo, a freqüência (em radianos/segundo) é exibida no eixo das abscissas em escala logarítmica. E no eixo das ordenadas, o valor do AR é convertido para a “escala de Bode”, com valores em decibéis. O método para traçar o diagrama pode ser resumido nas seguintes etapas:
- Determinar as frequências associadas aos pólos e zeros (ωp e ωz). Estas frequências equivalem aos módulos dos pólos e zeros de G(s). Marcar estes pontos no eixo das abscissas do gráfico.
- Calcular o ganho estático K de G(s), sabendo que K=G(0). No caso de obter K=0 ou K=inf, pular para o item 5.
- Converter o ganho estático K para “escala de Bode”, por meio da relação:
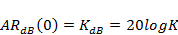
- O traçado de Bode começa sobre o eixo das ordenadas no valor KdB com um reta de inclinação nula no sentido crescente de ω. Ao passar por um ponto ω=ωp, a inclinação do traçado sofre um decréscimo de 20 dB/década. E, ao passar por um ponto ω=ωz , a inclinação sofre um acréscimo de 20 dB/década.
- Obter um ponto de referência calculando o valor da função 20log|G(jω)| em uma frequência ω qualquer (ex.: ω->inf ou ω->0), desde que resulte em uma valor real para a função. Marcar este ponto de referência no gráfico.
- Fazer o traçado seguindo a mesma orientação descrita no item 4, e de maneira que a linha cruze o ponto de referência.
- Procedimento para o diagrama de fase.
No gráfico de fase, a freqüência (em radianos/segundo) é exibida no eixo das abscissas em escala logarítmica. E no eixo das ordenadas, o valor do ângulo é dado em graus. O método para traçar o diagrama pode ser resumido nas seguintes etapas:
- Marcar os pontos ωp e ωz no eixo das abscissas do gráfico.
- Marcar sobre o eixo das ordenadas o ponto de partida 90(nz-np), onde nz é o número de zeros e np o número de pólos de G(s).
- Iniciar o traçado do ponto de partida com um reta de inclinação nula no sentido crescente de . Sempre uma década antes de ultrapassar uma abscissa ω=ωp, marcar um segundo ponto uma década após ω=ωp, com ordenada decrescida de 90 graus e traçar uma reta até este segundo ponto. E sempre uma década antes de ultrapassar uma abscissa ω=ωz, marcar um segundo ponto uma década após ω=ωz, com ordenada acrescida de 90 graus e traçar uma reta até este segundo ponto.
Resposta em freqüência de uma malha de controle
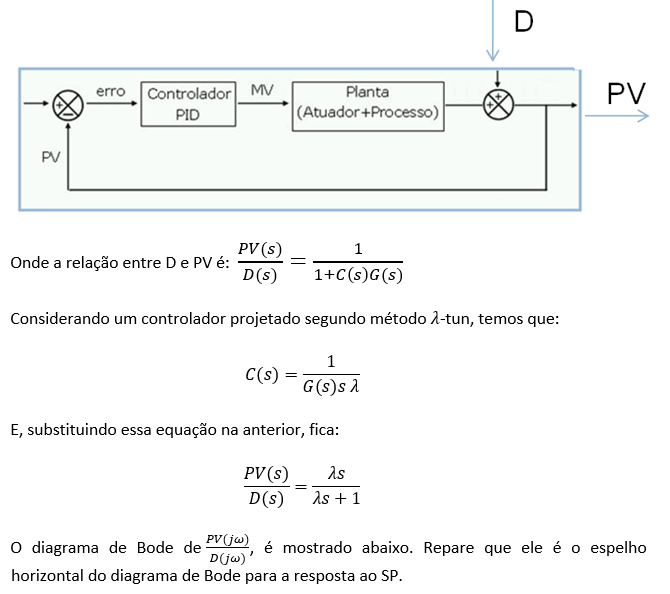
Nesta seção são destacadas dois tipos de resposta em frequência para uma malha de controle. Uma tomando como entrada o setpoint e outra o sinal de distúrbio somado à saída.
Considere o sistema retroalimentado e sua função de transferência para resposta ao Setpoint segundo projeto utilizando o método λ-tuning.

Um estudo de resposta em frequência irá revelar, por exemplo, a capacidade do sistema em rastrear um setpoint cíclico. Abaixo, o diagrama de Bode de GMF:

A banda de passagem é o intervalo de frequências do sinal de entrada (SP) que não sofrerão atenuação ao passar pelo sistema. Esta faixa corresponde ao intervalo entre zero e a freqüência de corte (ωc). Ou seja, se o sinal setpoint for senoidal, com frequência inclusa na banda de passagem, então teremos a situação ideal com atenuação nula (AR=1), e erro nulo (PV=SP).
![]()
Por outro lado, se a freqüência do setpoint estiver fora da banda de passagem, além da freqüência de corte, então AR<1 e, conseqüentemente, haverá atenuação e erro de controle. Isto ilustra a situação em que a malha de controle é incapaz de rastrear um setpoint pelo fato dele variar “rápido” demais.
Ainda observando o diagrama de Bode, para um setpoint com frequência 1 década após ωc a atenuação já é de 90% (AR=0,1) .
A segunda análise é a resposta em freqüência tomando como entrada o sinal de distúrbio (D) e saída a variável controlada (PV).
![]()
A banda de rejeição é o intervalo de frequências do sinal do distúrbio D que serão atenuadas pelo sistema. Esta faixa corresponde ao intervalo entre zero e a freqüência de corte (ωc). Ou seja, se o sinal do distúrbio for senoidal, com frequência inclusa na banda de rejeição, então o impacto na variável controlada será atenuado de acordo com o valor de AR mostrado na curva abaixo.
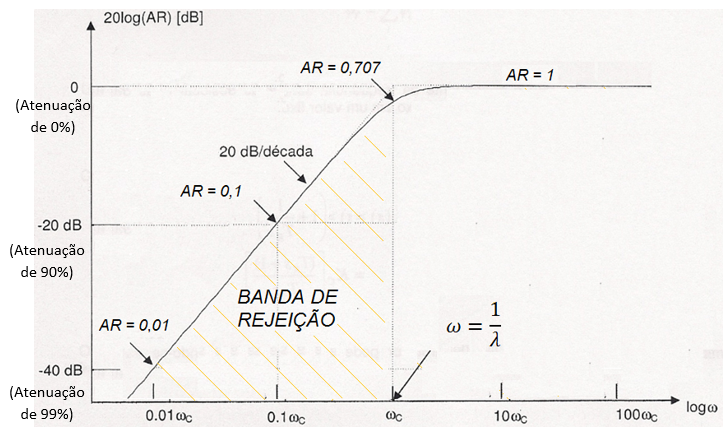
Alguns exemplos da relação entre a atenuação percentual e o AR:
- para AR=1, então PV=D, ou seja, atenuação de 0%
- para AR=0.1, então PV=0,1*D, ou seja, atenuação de 90%
- para AR=0.01, então PV=0,01*D, ou seja, atenuação de 99%
Projeto λ-tuning baseado em critérios de freqüência
O projeto consistem em escolher um valor para a frequência de corte ωc que resulte em uma banda de passagem ou banda de rejeição com largura adequada para o desempenho desejado.
Lembrando que: λ = 1/ωc
Exemplo 1: Considere uma malha de controle de posição em um manipulador robótico, que tenha como requisito rastrear um setpoint variável cuja frequência máxima é 0,5 Hertz. Considere ainda que o controlador é do tipo PID e projetado segundo método λ-tuning. Qual deve ser o valor de λ de maneira que o sistema opere sem erro de rastreamento?
Solução: Para que não haja atenuação entre os sinais de SP e PV, a freqüência de corte para a banda de passagem deve estar além da freqüência máxima de 0,5 Hz. Como já existe uma pequena atenuação no valor exato da freqüência de corte, então é considerado um valor 20% maior (0,6 Hz). Assim temos que:

Exemplo 2: Um forno industrial possui uma malha de controle para sua temperatura interna. Um de seus objetivos é compensar um distúrbio causado pela abertura periódica da porta. Considerando que a abertura da porta ocorre a cada 20 minutos, determine um valor de λ adequado para que este distúrbio sofra uma atenuação de pelo menos 90%.

Ineficácia do controle retroalimentado no ponto de vista da frequência
Foi mostrado no exemplo logo acima que para atenuar um distúrbio com período de 20 minutos, seria necessário um controlador que resultasse numa malha de controle extremamente rápida, com constante de tempo de apenas 19 segundos (quando valores típicos são de pelo menos 5 minutos para malhas de temperatura). Isto demandaria um sistema de compensação térmica de altíssima potência, difícil de ser implementado.
O fato é que sistemas retroalimentados são muito limitados para rejeitar distúrbios de carga. A tabela a seguir relaciona valores típicos para constante de tempo e tempo morto . Também consta o valor de λ para um controle sobreamortecido e o período de corte decorrente.

A próxima figura mostra a resposta em freqüência para cada um dos tipos de processos. Conforme já mencionado, uma atenuação de 90% só é atingida em períodos 10 vezes maiores que o período de corte (uma década antes de ωc) e uma atenuação total (99%) para períodos 100 vezes maiores (e duas décadas antes de ωc).